A legnagyobb értéke a kifejezés

Ahhoz, hogy megtalálja a legnagyobb értéke trigonometrikus kifejezések, sok esetben elegendő tudni, hogy a terület értékét szinusz, koszinusz, tangens, kotangens és tulajdonságai egyenlőtlenségeket.

Keresse meg a maximális értéke a kifejezés:

A tartomány a megengedett értékek ez a kifejezés - a teljes számot sor:

FIELD koszinuszértékeket - intervallum [-1; 1]. Annak megállapítására, az érték sokkal kényelmesebb használni a kettős egyenlőtlenséget:

Szorozzuk Terminusonként az egyenlőtlenség 7. Ha megszorozzuk a számos pozitív jel az egyenlőtlenség nem változik:

Ezután hozzáadjuk a Terminusonként 5:

Így a legmagasabb expressziós érték egyenlő 12 (a legkisebb - -2, terület értékek - [-2: 12]).

Megszorozva a negatív szám egyenlőtlenség jelek felcserélődnek:

Átírni növekvő sorrendben

Adjuk hozzá a Terminusonként 4

A legmagasabb expressziós érték egyenlő 7 (legalább - 1, az értéktartomány - [1, 7]).

A legmagasabb expressziós érték egyenlő 10 (a legkisebb - 8, az értéktartomány - [8, 10]).

(Megjegyzés: Ha az előre átalakítani a kifejezést .:

lehetőség van arra, hogy egyszerűsítse a vizsgálatnak, mivel nem szükséges, hogy szaporodnak az egyenlőtlenséget negatív szám) ebben az esetben.

Megoldás: A frakció értelme, ha a nevező nem nulla, így DHS: sinα ≠ 0. Az előnyös dolgozó DHS az egység kör: a pont α = 0 és α = P, amelyben sinα eltűnik. defekt:

Most lehet egyszerűsíteni a kifejezést, csökkentve azt

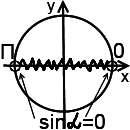
Továbbra is megbecsülni a kifejezést kapjuk.

Mivel azonban a DHS, van:

(Cosa = 1 α = 0, cosa = -1, ha α = P).

A kifejezés nem fogad el semmilyen maximális vagy a legkisebb érték (területe expressziós értékek - (8; 10)).

A következő alkalommal továbbra is figyelembe veszi a kifejezések frakciókkal, később - megnyilvánulásai formájában egy ∙ sinα + b ∙ cosa.