A mátrix megoldási módja rendszerek lineáris egyenletek (Slough oldatot használva egy inverz mátrixot)

Ebben a cikkben, beszéljünk a mátrix módszer megoldására rendszerek lineáris algebrai egyenletek az űrlap

, amely mátrix formában írható fel, ahol - az alapvető mátrix rendszer, - egy oszlop mátrix ismeretlen változó - a mátrix abszolút értelemben.

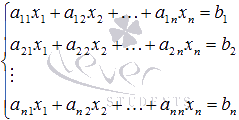
Először leírjuk a lényege a mátrix módszer, nézzük a feltétellel alkalmazható-e ez a módszer, részletesebben elemzik oldatok néhány példát.

Oldalnavigáció.

A mátrix megoldási módja rendszerek lineáris algebrai egyenletek - levezetése.

Tegyük fel, hogy egy inverz mátrixot mátrix a rend n és n. Szorzása mindkét oldalán a bal oldalon a mátrix-egyenlettel (megrendelések mátrixok ⋅ X és B teszi, hogy ezt a műveletet, lásd a cikk műveletek mátrixok tulajdonságait műveletek). Van. Mivel a művelet a szorzás a mátrixok megfelelő sorrendben asszociatív jellemző tulajdonság, az utóbbi egyenlet átírható, mint, és definíció a fordított mátrix (E - azonosító mátrix a rend n-n), így

Így a megoldás a lineáris egyenletrendszer által mátrix módszer határozza meg a képlet. Más szóval, a megoldás SLAE segítségével a fordított mátrixba.

Tudjuk, hogy egy négyzetes mátrix A rend n n mátrix inverz ha determinánsa nem nulla. Következésképpen, egy rendszer n lineáris algebrai egyenletek n ismeretlennel mátrix módszer lehet megoldani, ha a meghatározó a fő mátrix rendszer nem nulla.

Példák a megoldására rendszerek lineáris egyenletek segítségével a mátrix módszer.

Tekintsünk egy mátrix módszer példával. Egyes esetekben, akkor nem írja le részletesen a folyamat számítási meghatározó mátrixok, ha szükséges, olvassa el a cikket, a számítás a meghatározója a mátrix.

A rendszer egyenletek mátrix formában van. Kiszámítjuk a meghatározója a fő mátrix a rendszer, és győződjön meg arról, hogy a nullától eltérő:

Másodfokú polinom nem nulla semmilyen valós értékeket, mivel a diszkrimináns negatív, így a fő meghatározója a mátrix rendszer nem egyenlő nullával alatt érvényes. Mátrix módszerekkel van. Mi megépíteni a fordított mátrix által a képlet:

Javasoljuk, hogy ellenőrizze az eredményt.

.

A mátrix módszer megoldására lineáris rendszerek, amelyekben a számú egyenlet egyenlő száma ismeretlen változók és a determináns, a fő mátrix a rendszer nullától eltérő. Ha a rendszer több mint három egyenletet, megtalálni az inverz mátrix igényel jelentős számítástechnikai tevékenység, így ebben az esetben célszerű használni a módszert, hogy megoldja a Gauss.