Fuzzy halmazok és azok jellemzői

Fuzzy (vagy homályos, zavaros) set - fogalma szerint Zadeh LA, kibővített klasszikus (Cantor) fogalmát meg, feltételezve, hogy a karakterisztikus függvény (tagsági függvény elemkészlet) bármilyen értéket felvehet a [0,1] intervallumban, és nem csak az értéket 0 vagy 1.

Definíció. fuzzy halmaz (fuzzy set)

Legyen C egy univerzális szett (univerzum). Ezután a fuzzy halmaz A-C meghatározása szerint olyan rendezett párok halmaza

ahol nevezett tagsági függvény (AF) egy elem x a fuzzy halmaz A.

AF rendel minden egyes eleme a C értéket a [0, 1], amely az úgynevezett fokú tagság X az A vagy a fuzzy intézkedés.

Fuzzy intézkedés lehet tekinteni, mint egy bizonyos fokú igazság, hogy az x elem tartozik A.

Definíció. fuzzy halmazok (a támogatás egy fuzzyset)

A fuzzy halmaz halmaza pontokat úgy, hogy.

Így a meghatározása fuzzy halmaz egy kiterjesztése a klasszikus meghatározás készlet, ahol a karakterisztikus függvény vehet folyamatos értékek 0 és 1 közötti A világegyetem C lehet diszkrét vagy folytonos készlet.

Képviseletére AF általában használt többféle parametrikus funkciókat.

Tipikus bemutatása AF

Háromszögű OP (. 2.2 ábra a) leírja a három paraméter a, b, c>, amelyek meghatározzák x koordinátáit a három háromszög szögei az alábbiak szerint:

Trapéz alakú OP (. 2.2 ábra c) leírása négy paraméter a, b, c, d>, amelyek meghatározzák x koordinátáit a négy sarkából a trapéz a következőképpen:

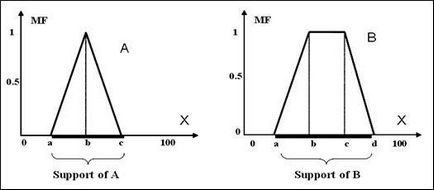
Ábra. 2.2. Háromszög és trapéz OP

Gauss OP (. 2.3 ábra) által meghatározott két paraméter, és képviseli az alábbi funkciót.

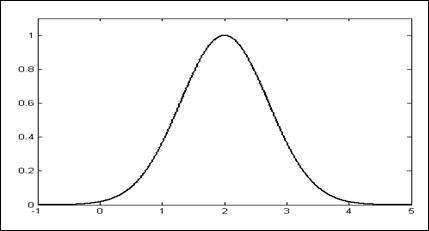
Ábra. 2.3. Gauss OP

Az egyik alapvető fogalmakat bevezetni Zadeh, a koncepció a nyelvi változó.

Definíció. nyelvi változó (PL) képviseli a következő öt. ahol - a változó nevét - távon beállított, előre megadott LP értékek nyelvi kifejezések (szintagmák), X - világegyetem, a G - szintaktikai szabály, mely segítségével tudjuk alkotnak szintagma. M - szemantikai szabály alkalmazásával minden szintagma annak köszönhető, hogy az értéket, amely a fuzzy halmaz az univerzum X.

Egy példa a PL lehet, például változó = „kor”. Idejének készlet lehet például a következő:

(Életkor) = nagyon fiatal. fiatal. több vagy kevesebb fiatal. középkorú. régi. nagyon régi>.

Mert ebben az univerzumban LP szolgálhat a valós számok halmaza, például az intervallum. M rendel szemantikai szabály therms a T (régi) értékek, amelyek a különböző módosítások fuzzy halmazok.

Visszatérve a példában a jármű mozgásának ellenőrzése és leírják a nyelvi értékek a fenti szabályok alkalmazásával fuzzy halmazok. Tekintsük a következő nyelvi változók:

X - a járművek közötti távolság;

y - sebesség lovas kocsi előtt;

z - jármű gyorsulását kezelt.

AF kell meghatározni összhangban tartják az irányítást a helyzet. Például egy sebessége 70 km / óra, a „nagy” a közlekedési helyzet az úton, és a város is tekinthető „kis” a közlekedési helyzet az autópályán.

Mi határozza meg a mi például a következő univerzumok:

Ábra. 2.4 OP látható, hogy leírja a nyelvi értékek „kis» (lassú) és a „nagy» (gyors) a sebesség és a „közeli» (rövid) és a „nagy» (hosszú) a távolságot.

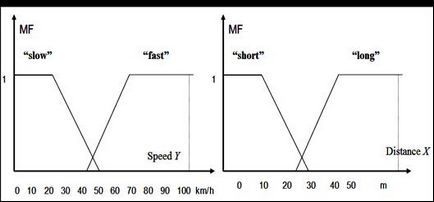
Ábra. 2.4. Fuzzy halmazok egyszerű jármű mozgásának ellenőrzési feladatok

Különbségek a klasszikus és fuzzy halmazok képviselet

Vegyük sorra ezeket különbségeket az alábbi példa. Tekintsük a klasszikus és fuzzy halmaz ábrázolások leírni a nyelvi értékek „rövid” (a távolság).

Ábra. 2.5 közötti különbségeket mutatja be a klasszikus és a fuzzy képviselete több Egy ennek a példának.

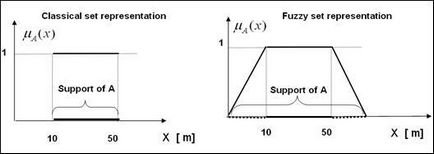
Ábra. 2.5. Klasszikus és fuzzy ábrázolások A halmaz

Mi határozza meg a klasszikus ábrázolása A halmaz, ábrán látható. 2.5 maradt. Ebben az esetben, a jellemző függvény:

A ábrázolása fuzzy halmazok ábrán látható. 2.5 Jobb. Ebben az esetben az AF funkció tartozékok, az alábbiak:

Most, hogy a következő kérdést. hogy a pont tartozik az m vagy m mnozhestvuA pont?

Abból a szempontból a klasszikus ábrázolása a válasz „nem”. A szempontból az emberi érzékelés helyett a válasz „igen”, mint a „nem”. A szempontjából fuzzy képviselete a válasz „igen”.

Így ez az egyszerű példa azt mutatja, hogy a fuzzy megközelítés inkább közel áll a természetes, emberi, és rugalmasabb, mint a klasszikus megközelítés.

A rendszer segítségével a fuzzy halmazok, le tudjuk írni a fuzzy határokat.

Alapvető műveletek elmélete fuzzy halmazok

Mi határozza meg az alapvető fuzzy művelet következik.

Definíció: Egy fuzzy részhalmaza (Fuzzy Containment vagy Fuzzy részhalmaz). A fuzzy halmaz tartalmaz egy fuzzy halmaz B (vagy ezzel egyenértékűen, A jelentése egy részhalmaza B), ha és csak akkor, ha az összes. Szimbolikus formában:

Definíció: Az egyenértékűség fuzzy halmazok (Egyenlő Fuzzy Sets). Ekvivalencia (egyenlőség) fuzzy halmazok A és B jelentése a következő:

Definíció: fuzzy unió vagy fuzzy diszjunkció (Fuzzy Union) .Obedinenie két fuzzy halmaz A és B (szimbolikus formában vagy írásbeli, illetve B vagy A B) egy fuzzy halmaz. AF meghatározása a következő:

Definíció: fuzzy kereszteződés (Fuzzy kereszteződés) metszéspontja a csökkenő két fuzzy halmazok A és B (szimbolikus formában vagy írva, mint C = A és B vagy C = A B.) Van egy fuzzy halmaz. AF meghatározása a következő:

Definíció: a fuzzy kívül. Supplement A (szimbolikusan írva, mint vagy a) nem világos, AF a következőképpen határozzuk meg:

2.6 ábra mutat példát, fuzzy műveletek fuzzy halmazok.

Ábra. 2.6. Példák fuzzy műveletek fuzzy halmazok

Jellemzők fuzzy halmazok

Megjegyzés: a legfontosabb jellemzője az elmélet fuzzy halmazok.

1) A törvény a kizárt harmadik és a törvény kontradiktsii. ahol - igaz, hogy az üres halmaz a klasszikus halmazelmélet, hanem az elmélet a fuzzy halmazok, általában nincsenek megelégedve.

Törvény a kizárt közepén, és a törvény kontradiktsii fuzzy elmélet a következő: és.

2) A több klasszikus halmazelmélet dot lehet egy két lehetőség van: vagy. A fuzzy elmélet pont tartozhat a halmaz, és ezzel egyidejűleg tartoznak (azaz tartoznak a beállított) különböző értékeket tagsági függvényeket és. ábrán látható. 2.7.

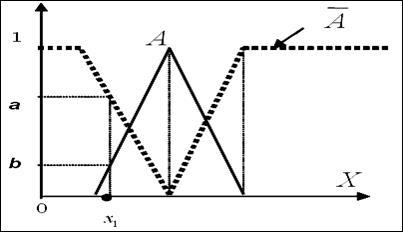
Ábra. 2.7. Feature fuzzy halmazok

Ez azt jelenti, hogy a folyamat a fuzzy érvelés, tudunk egyszerre vizsgálni két lehetőség van, ami az érvelés folyamat rugalmasabb, mint a klasszikus.

3) kapcsolat az elmélet a valószínűség. Az elmélet a fuzzy halmazok bizonyos értelemben csökken az elmélet véletlen készletek, és így a valószínűségszámítás. SZEKVENCIA LEÍRÁSA leíró elmélet ez a csökkenés, kívül esik e könyv [lásd. Linkek a honlapon Wikipedia]. Az alapötlet az, hogy az érték a tagsági függvény lehet tekinteni, mint a valószínűsége, hogy a burkolóelem néhány véletlenszerű halmaza B. azonban a gyakorlati alkalmazás a készülék fuzzy halmazok elmélete általában önmagában, beszélt a versenyző a készülék valószínűségszámítás, statisztika.