Grafikus módszer - lineáris programozás

A módszer leírása

Ha csak két változó lineáris programozási probléma, akkor meg lehet oldani a grafikus módszerekkel.

Tekintsük meg a problémát a lineáris programozás két változó, és.
(1.1);
(1.2)
Itt van. vannak önkényes számokkal. Ez a cél lehet akár, hogy megtalálják a maximális (max), és a meghatározást a minimális (min). A rendszer korlátai lehetnek jelen jelei. és a jelek.

A építési terület megvalósítható megoldásokat

Grafikus módszer a probléma megoldására (1) az alábbiak szerint.
Eleinte töltünk a tengelyeket és és válassza ki a skála. Mind a rendszer korlátaira egyenlőtlenségek (1.2) határozza meg a félsík behatárolja a megfelelő egyenes vonal.

Tehát, az első egyenlőtlenség
(1.2.1)
Ez határozza meg a félig sík által határolt vonal. Az egyik oldalon a sorban. és a másik oldalon. A nagyon közvetlen. Ahhoz, hogy megtudja, melyik oldalon a egyenlőtlenség (1.2.1), úgy döntünk, egy tetszőleges pont nem a vonalon. Ezután azt helyettesíteni koordinátáit ebben a kérdésben (1.2.1). Ha az egyenlőtlenség teljesül, a fél-sík tartalmazza a kiválasztott ponthoz. Ha az egyenlőtlenség nem teljesül, a félig síkban található, a másik oldalon (nem tartalmazza a kiválasztott pont). Half-árnyék, amelyre az egyenlőtlenség (1.2.1).

Ugyanezt elvégezzük a rendszer többi része egyenlőtlenségek (1.2). Így megkapjuk az árnyékos félsíkra. megvalósítható megoldásokat tájékozódási pont kielégíti az összes egyenlőtlenségek (1.2). Ezért, grafikusan, a terület a megvalósítható megoldásokat (SDT) metszéspontja az összes épített félig síkok. SDT árnyékban. Ez egy konvex sokszög, akiknek az arca tartoznak építve. SDT is lehet határtalan konvex alakja, szegmens, ray, vagy a vonal.

Ez adódhatnak olyan esetben, amikor a félig sík nincs közös pont. Ezután a terület megvalósítható megoldásokat üres. Ezt a problémát nem megoldás.

Lehetőség van, hogy egyszerűsítse a módszert. Nem lehet árnyékolás félóránként sík, és az első építeni minden közvetlen
(2)
Ezután válasszon egy tetszőleges pont, nem tartozik semmilyen ezeket a sorokat. Helyettesítsük koordinátáit ezen a ponton a rendszer egyenlőtlenségek (1.2). Ha minden egyenlőtlenségek teljesül, akkor a lehetséges régiót határolt építve, és magában foglalja a kiválasztott ponthoz. Shade a megvalósítható régió közvetlen határokat úgy, hogy az magában foglalja a kiválasztott ponthoz.

Ha bármelyik feltétel nem teljesül, akkor válasszon egy másik ponton. És így tovább, amíg egy pont is található, amelynek koordinátái kielégítik (1.2).

Megtalálni a szélsőérték a célfüggvény

Tehát van egy árnyékos területen megvalósítható megoldásokat (SDT). Ez korlátozza a sokszögű vonal tartozó épített egyenes vonalak, és amely gerendák (2). SDT mindig domború. Ez lehet egy korlátos halmaz, és nem korlátozódik mentén meghatározott irányban.

Most már tudjuk keresni extrémuma a célfüggvény
(1.1).

Ehhez válassza ki tetszőleges számú és épít a közvetlen
(3).
Az egyszerűség kedvéért a további hisszük, hogy ez a vonal áthalad az SDT. Ezen a vonalon az objektív függvény állandó és egyenlő. ez a sor az úgynevezett vonal szintű funkciókat. Ez a vonal osztja a síkot két fél-sík. Egy félsíkra
.
Másrészt félsíkra
.
Ez az egyik oldalon a vonal (3) a célfüggvény növekszik. És tovább is otodvinem pont a vonal (3), annál nagyobb az értéke. A másik oldalon a vonal (3) az objektív függvény csökken. És tovább is otodvinem pont a vonal (3) a másik irányba, minél kisebb az érték. Ha húzunk egy vonalat a vonal mentén (3), az új vonal is irányítja a szint a célfüggvény, de egy másik értéket.

Így, hogy megtalálják a legnagyobb érték a célfüggvény, szükséges, hogy dolgozzon egy párhuzamos egyenes vonal (3), a maximális távolság, hogy abba az irányba növekvő értékeket. és átnyúlik legalább egy ponton a SDT. Ahhoz, hogy megtalálja a minimális érték a célfüggvény, szükséges, hogy dolgozzon egy párhuzamos egyenes vonal (3) és egy maximális távolság belőle irányába csökkenő értékek. és átnyúlik legalább egy ponton a SDT.

Ha SDT korlátlan, előfordulhat olyan eset, amikor egy egyenes vonal nem tudja tartani. Azaz, nem számít, hogyan eltávolítottuk közvetlenül a szintet a sor (3) irányában növekvő (csökkenő). majd a sort mindig áthalad az SDT. Ebben az esetben lehet tetszőlegesen nagy (kicsi). Ezért a maximális (minimális) értéke nem. így a probléma nem.

Vegyük azt az esetet, amikor egy szélsőséges párhuzamos egyenes bármely vonal formájában (3), áthalad az egyik a sokszög csúcsai SDT. A grafikon meghatározzuk a csúcsainak koordinátáit. Ekkor a maximális (minimális) értéke a célfüggvény adja meg:
.
megoldás a probléma
.

Azt is megfelelnek az esetben, ha a vonal párhuzamos egyik arca az SDT. Ezután a vonal megy át két sokszög csúcsait a SDT. És meghatározza a koordinátáit azok a pontok. Ahhoz, hogy meghatározzuk a maximális (minimális) értéke a célfüggvény lehet használni ezeket a koordinátákat csúcsok:
.
Probléma végtelen sok megoldás. A megoldás, hogy bármely pontján található, a szegmens között a pontokat, és. többek között a pontok maguk.

Egy példa a probléma megoldásának a lineáris programozás grafikus módszerrel

állapot probléma

A cég egy ruhát két A és B modellre használata háromféle szövetben. A gyártás a ruha minta Egy igényel 2 m az első fajta szövet, a szövet 1 m a második fajta, 2m harmadik típusú szövet. A gyártás a ruha minta szükséges a szövet 3 m az első fajta, m 1 második szövedék formájában 2 m harmadik típusú szövet. Készletek az első típusú szövet 21 m, a második faj - 10 m, a harmadik típusú -. 16 m Issue egyik terméktípus A bevételt 400 den. u egy termék B típusú - 300 den. u

Készítsen termelési terv, amely a vállalat a legtöbb bevételt. Által megoldott probléma grafikus módszerekkel.

Hagyja, hogy a változók és azt az összeget jelenti ruhák modellek A és B, ill. Ezután fordított összeg az első típusú szövet:
(M)
A használt mennyiség a második típusú szövet:
(M)
A felhasznált térfogata harmadik fajta szövet lesz:
(M)
Mivel a termelt mennyisége ruhák nem lehet negatív, akkor
és.
Bevétel a díj lesz:
(Den. Egység).

Ezután a gazdasági és matematikai modellje a probléma a következő:

Mi megoldjuk a grafikus módszer.
Döntetlen koordinátatengellyel.

Épület egy egyenes vonal.
Amikor.
Amikor.
Egyenes vonal húzása ponton át (0, 7) és a (10,5, 0).

Épület egy egyenes vonal.
Amikor.
Amikor.
Egyenes vonal húzása ponton át (0; 10) és a (10, 0).

Épület egy egyenes vonal.
Amikor.
Amikor.
Rajzolj egy egyenest a (0, 8) és (8, 0).

Közvetlen és koordinátatengelyeken.

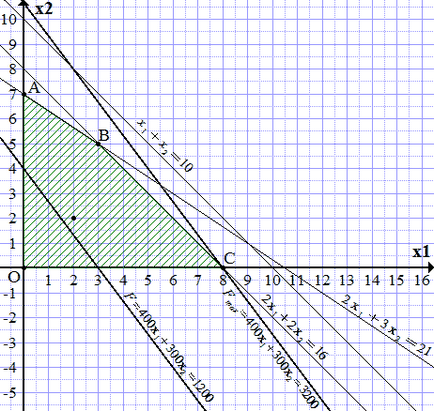
FIELD megvalósítható megoldásokat (SDT) határolja vonalak kialakítani és koordinátatengelyek. Ahhoz, hogy megtudja, melyik oldalon azt látjuk, hogy az a pont tartozik az SDT, mint kielégíti a egyenlőtlenségrendszer:

Shade területen arra a pontra (2, 2) nyomja a vonalkázott rész. Kapunk négyszög OABC.

Épület tetszőleges szintvonal a célfüggvény, pl,
(A1.1).
Amikor.
Amikor.
Egyenes vonal húzása ponton át (0, 4) és a (3, 0).

Továbbá azt megjegyezni, hogy mivel az együtthatók a pozitív és a célfüggvény (400 és 300), növeli u. Egy egyenes párhuzamos a vonal (A1.1) a maximális távolságot úgy irányába növekvő. és átnyúlik legalább egy pont egy négyszög OABC. Az ilyen egyenes vonal áthalad a C pontban az építési meghatározza a koordinátáit.
.

Azaz, hogy a legnagyobb bevételt, meg kell, hogy ruhák 8 modell A. A bevétel eléri majd 3200 den. u

állapot probléma

Hogy oldja lineáris programozási feladatok grafikus módszerekkel.

Mi megoldjuk a grafikus módszer.
Döntetlen koordinátatengellyel.

Épület egy egyenes vonal.
Amikor.
Amikor.
Egyenes vonal húzása pontokon keresztül (0, 6) és a (6 0).

Épület egy egyenes vonal.
Itt van.
Amikor.
Amikor.
Egyenes vonal húzása ponton át (3, 0) és (7, 2).

Épület egy egyenes vonal.
Épület egy egyenes vonal (x-tengely).

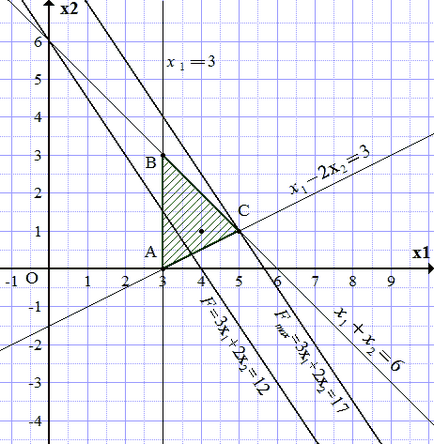
FIELD megvalósítható megoldásokat (SDT) korlátos kialakítva egyenes. Ahhoz, hogy megtudja, melyik oldalon azt látjuk, hogy az a pont tartozik az SDT, mint kielégíti a egyenlőtlenségrendszer:

Árnyékolás terület határait épített egyenes vonalak egy pontban (4; 1) megüt a vonalkázott rész. Kapunk az ABC háromszög.

Épület tetszőleges szintvonal a célfüggvény, pl,
.
Amikor.
Amikor.
Egyenes vonal húzása át a szinten a pont (0, 6) és a (4 0).
Mivel az objektív függvény növekszik és. húzunk egy vonalat párhuzamos vonal szint és a legnagyobb távolság azt az irányt növekszik. és átnyúlik legalább egy ponton a háromszög AVC. Az ilyen egyenes vonal áthalad a C pontban az építési meghatározza a koordinátáit.
.

Egy példa a megoldások hiánya

állapot probléma

Problémák a lineáris programozási feladat grafikusan. Keresse meg a legnagyobb és legkisebb érték a célfüggvény.

Mi a probléma megoldására a grafikus módszer.
Döntetlen koordinátatengellyel.

Épület egy egyenes vonal.
Amikor.
Amikor.
Rajzolj egy egyenest a (0, 8) és (2.667, 0).

Épület egy egyenes vonal.
Amikor.
Amikor.
Egyenes vonal húzása pontokon keresztül (0, 3) és a (6 0).

Épület egy egyenes vonal.
Amikor.
Amikor.
Egyenes vonal húzása ponton át (3, 0) és (6, 3).

Közvetlen és koordinátatengelyeken.

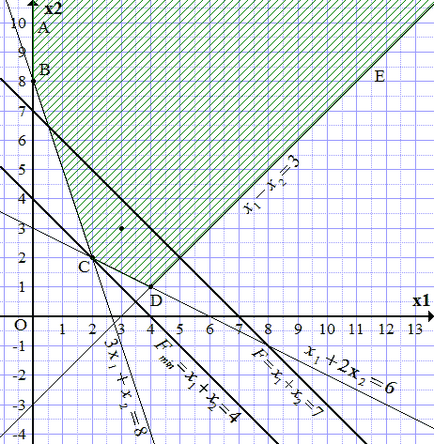
FIELD megvalósítható megoldásokat (SDT) határolja vonalak kialakítani és koordinátatengelyek. Ahhoz, hogy megtudja, melyik oldalon azt látjuk, hogy az a pont tartozik az SDT, mint kielégíti a egyenlőtlenségrendszer:

Shade területen arra a pontra (3, 3) betoljuk a árnyékolt része. Get korlátlan domain által határolt szaggatott vonal ABCDE.

Épület tetszőleges szintvonal a célfüggvény, pl,
(A3.1).
Amikor.
Amikor.
Egyenes vonal húzása pontokon keresztül (0, 7) és a (7, 0).
Mivel az együtthatók pozitív, majd együtt növekszik, és.

Ahhoz, hogy megtalálja a maximális, meg kell felhívni a párhuzamos vonal, a legtávolabbi irányába növekszik. és átnyúlik legalább egy ponton a terület ABCDE. Azonban, mivel a terület korlátlan a magas értékek és. hogy az ilyen magatartás nem lehet egyenes. Bármi vonal már nem végeznek, mindig lesznek a terület egy pont távolabbi irányába növekszik, és. Ezért nincs maximum. Ez lehet tetszőlegesen nagy.

Keresünk legalább. Egy egyenes párhuzamos a vonal (A3.1) és a legtávolabbi belőle irányába csökken. és átnyúlik legalább egy ponton a terület ABCDE. Az ilyen egyenes vonal áthalad a C pontban az építési meghatározza a koordinátáit.
.
A minimális érték a célfüggvény:

A maximális érték nem létezik.
minimális érték
.