Grafikus módszer megoldására ZLP Online
A lineáris programozás segítségével grafikus módszerrel, amellyel meghatározzák konvex halmazok (oldatok poliéder). Ha az alapvető probléma a lineáris programozás az optimális terv, a célfüggvény értéket vesz fel az egyik csúcsot a poliéder megoldások (lásd. Ábra).
Utasításokat. Jelölje a sorok számát (a szám a korlátok). Ha az összeg több mint két változó, szükséges, hogy a rendszer SZLP (cm. És példák №2). Ha kettős restrikciós, például 1 ≤ x1 ≤ 4. két részre van osztva: x1 ≥ 1. x1 ≤ 4 (azaz, a sorok száma növekszik 1).
Építsd terület megengedett megoldások (SDT) is használhatja ezt a szolgáltatást.
Példa a Word
Együtt a számológép is használja a következő:
A döntési mátrix játék
Segítségével a szolgáltatást az interneten, akkor meg az ár egy mátrix játék (alsó és felső határa), ellenőrizze a nyereg pont megoldást találni vegyes stratégiát módszerek: Minimax, szimplex módszer, grafikus (geometrikus), az eljárást a Brown.
- A gépen X1 0x2 építeni közvetlen.
- Határozza meg a félig sík.
- Adjuk meg a poligon-készítés;
- Építsünk vektort N (C1, C2), ami azt jelzi, az irányt a célfüggvény;
- Mozgatja az objektív függvény közvetlenül C1 x2 + c2 x2 = 0 az irányt a vektor N ponton a sokszög megoldásokat.
- Kiszámítása koordináta pont, és az értéke a célfüggvény ezen a ponton.
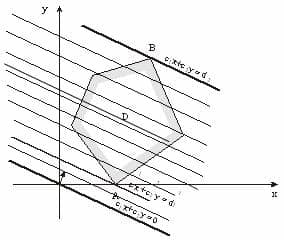
A következő esetek fordulhatnak elő:
- A célfüggvény feltételezi szélsőséges (maximum vagy minimum) érték egypontos A.
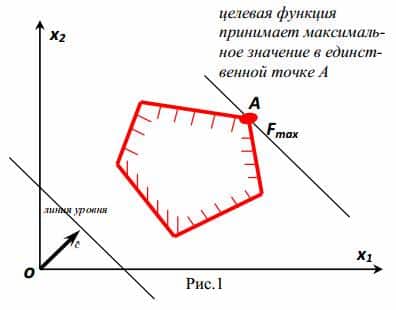
- A cél függvény szélsőérték bármely pontján az AB szakasz.
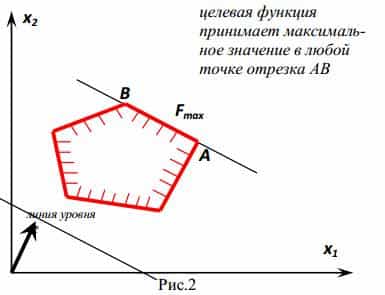
- A célfüggvény nem határolja a fenti (ha nézi a maximum) vagy az alatt (legalább)
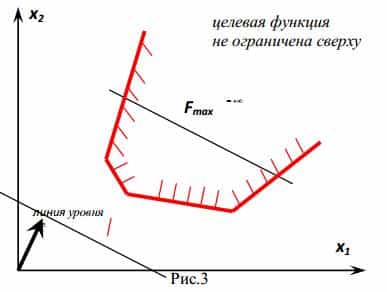
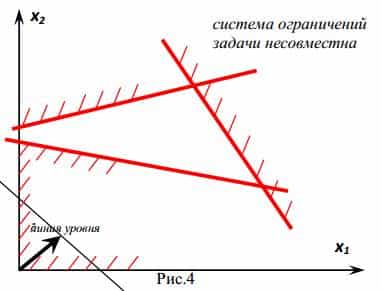
- A rendszer korlátozza a probléma következetlen
Példa. A cég gyárt kétféle termék - P1 és P2. Az alkalmazott termelési kétféle alapanyag - a C1 és C2. Nagykereskedelmi egységár egyenlő 5 CU A P1 és 4 CU P2. Fogyasztás nyersanyagok egységnyi kibocsátás típusú P1 és P2 típusú a táblázatban megadott.
Táblázat - a fogyasztás a nyers anyagok gyártása
A fogyasztás a nyersanyagok 1 egység. termékek
Maximális leltár a nyersanyagok, egységek.