lineáris egyenletek

A száma gyökerek, függetlenül attól, a és b:

- Amikor a = b = 0. ez azt jelenti, hogy az egyenletnek végtelen számú megoldást ettől.

- Amikor a = 0. b ≠ 0 azt jelenti, hogy az egyenletnek nincs gyökerei.

- Ha a ≠ 0 azt jelenti, hogy az egyenletnek csak egy gyökér.

Lineáris egyenlet két változó között.

Egyenletben x változó egyenlő típusú A (x) = B (x). ahol A (x) és B (x) - kifejezések x. Ha ebben az esetben értékek a beállított T x egyenletet kapjuk igaz numerikus egyenlőség, amely az úgynevezett egy sor igazság vagy a megoldást erre adott egyenlet egyenlet. és az összes ilyen változó érték - a gyökerek az egyenlet.

Lineáris egyenletek 2 változók a következő formában:

- általános formában: ax + by + c = 0,

- kanonikus formában: ax + by = -C,

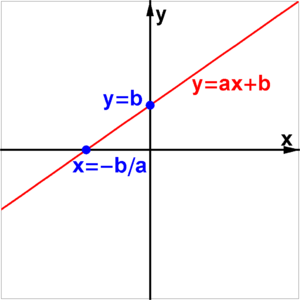
- formájában egy lineáris függvény: y = kx + m. hol.

Határozata vagy gyökerek az egyenlet egy pár változó értékek (x; y). ami kiderül, hogy a személyazonosság. Ezek a megoldások a (gyökerek) a lineáris egyenlet 2 korlátlan számú változók. Geometriai modell (egy grafikon) közvetlen egyenlet y = kx + m.

Ha az egyenletet X négyzete, akkor ezt az egyenletet nevezzük másodfokú egyenlet.