másodfokú függvény
Ha szilárdan rögzítse az általános ismereteket a funkciót (kijelölési módszerek, grafikai koncepció) további vizsgálatot más típusú funkciók kapnak sokkal könnyebben.
Az úgynevezett másodfokú függvény
Másodfokú függvény - függvényében formájában
ahol a. b és c - az adott számmal.
Más szóval azt mondhatjuk, hogy ha egy régebbi funkció (azaz a legnagyobb), hogy milyen mértékben van „x” - ez a „2”, akkor van egy másodfokú függvény.
Tekintsük a példát kvadratikus függvények, és meghatározza, mik azok egyenlő együtthatók „a”, „b” és „c”.
A grafikon a másodfokú függvény az úgynevezett parabola.
Parabola következők.
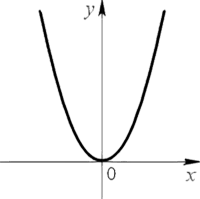
Is lehet fordított parabola.
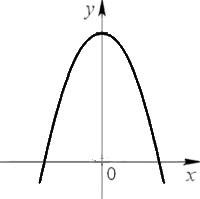
Hogy könnyebb megérteni az algoritmus, csak megmagyarázni egy példát.
Készítünk egy grafikon a másodfokú függvény «y = x 2 -7x + 10" .
- Az irányt a parabola ágai
Ha «a> 0" , az ág felfelé irányuljon.
Ha «2 -7x + 10" .
Most meg kell találnunk «y0» (csúcsainak koordinátáit a «Oy» tengely). Ehhez helyettesítse a talált érték «x0» az eredeti funkciót. Emlékszem, hogyan kell megtalálni a függvény értéke lehet a leckét a „Hogyan oldja meg a problémát a funkció” alatt „Ahhoz, hogy az a függvény értékét.”
y0 (3,5) = (3,5) 2-7 3,5 · 10 = 12,25 + - 24,5 + 10 = -12,25 + 10 = -2,25
Írja ki a koordinátákat a csúcsa a parabola kapunk.
(·) A (3,5; -2,25) - csúcsa a parabola.
Megjegyzés parabola csúcsa a koordináta-rendszerben. Keresztül a szimmetria tengelye a bázispontot, mint egy parabola - jelentése szimmetrikus grafikon «Oy» tengelyen.
Először is, nézzük meg, mi az úgynevezett nulla.
Nullák - ez a grafikon a metszéspontok tengelyével «Ox» (x tengely).
Nyilvánvaló nullák a diagram így néz ki:
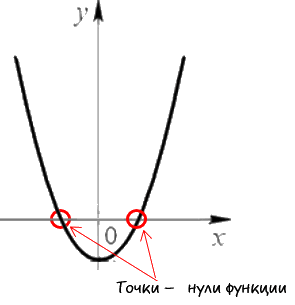
A név a nullák kapott annak a ténynek köszönhető, hogy ezek a pontok a koordináta «Oy» tengely nulla.
Most nézzük meg, hogyan kell a rajzoló funkciókat kiszámításához a pontok koordinátái nullák.
Ahhoz, hogy megtalálja a koordinátákat a nullák, meg kell, hogy helyettesítse az eredeti funkciója «y = 0" .
Behelyettesítve egy előzetesen meghatározott függvény «y = x 2 -7x + 10" helyett« y = 0" és oldja a kapott másodfokú egyenlet «X».
0 = X 2 -7x + 10
x 2 -7x + 10 = 0
x1; 2 =
7 ± √ 49-4 × 1 · 10