Piramis, amelyben a torziós szögek egyenlő alapon
Most tekintsük a piramis, amelyben a torziós szögek tövében egyenlő azzal, amit azok tulajdonságait képviseli.
Ha az összes diéderes szögek a széleken a bázis egyenlő. az
1) a csúcsa a piramis az előrejelzések közepén a beírt kör a bázis;
2) Az alap a piramis a merőleges vetülete az oldalfelületén. Azonban piramis bázis területen megtalálhatók a következő képlettel
- A diéderes szög alatt az alapja a piramis. A legtöbb esetben ezt a képletet használják, hogy megtalálják a terület az oldalsó felületén a piramis:
Ennek megfelelően, a teljes felülete a piramis
3) palástfelületén a jelen esetben is megtalálható a következő képlettel
ahol p - semiperimeter bázis, l - magassága a laterális szélén levonni a csúcsa a piramis.
A téglalap alakú háromszögek által képzett a piramis magassága, a magasból az oldalfelületek levonni a tetején a piramis és nyúlványok (egyenlő a sugara a beírt kör) egyenlő. ezért is
- a magassága a oldalfelületek levonni a csúcsa a piramis, egyenlő;
- a magassága a oldalfelületek képező piramis, amelynek magassága egyenlő szögek.
Problémák megoldása egy piramis, amelyben a diéderes szögek a bázis egyenlő (vagy - piramis, amelyben a magassága a oldalfelületet vagy kialakítva, amelynek magassága egyenlő szögek piramis), kezdődik a rajz.
Ha az alapja a piramis - háromszög
A központ írt kör a háromszög fekszik szigorúan a háromszög és a metszéspontját bisectors azt.
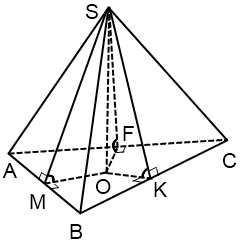
A sugara a beírt kör keres képletű
ahol S - a háromszög területe, p - a padló kerülete.
Ha az alapja a piramis egy derékszögű háromszög. rajz egy kicsit más.
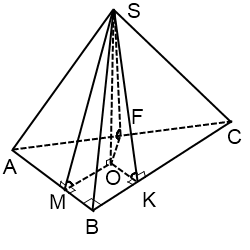
A sugara a beírt kör a téglalap alakú háromszög keres képletű
ahol a és b - a lábak, c - átfogója.
Ha az alapja a piramis - paralelogramma
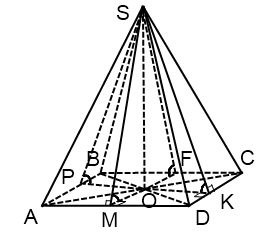
O - a metszéspontja az átlók egy rombusz (négyzet).
A sugara a beírt kör a gyémánt megtalálható az alábbi képlet szerint
Sőt, a sugara a beírt kör a rombusz fele a magassága.
Ha az alap a piramis - egy tetszőleges négyszög
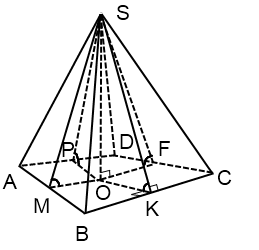
Mintegy - a metszéspontja a szögfelezői ABCD.
A kör sugara írt a négyszög keresi ugyanazt a formulát
Ahogy írva a négyszög körben lehetséges akkor, ha az összeg a hossza az ellenkező oldalán azonos,
Ha az alapja a piramis - Keystone
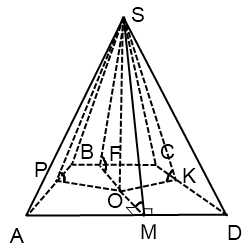
O - a metszéspontja a szögfelezői a trapéz.
A kör sugara írt trapéz
és a sugara a beírt kör felével egyenlő a magassága a trapéz.
Ha az összes diéderes szögek alján a piramis egyenlő (vagy magassága az oldalfelületek a piramis egyenlő, vagy a magassága az oldalfelületek a piramis, hogy az egyenlő szögek), és az alján a piramis - egy szabályos sokszög, ez - rendszeres piramis.