Raspredelenie Puassona 2
Valószínűségszámítás - matematikai tudomány, hogy a tanulmányok a minták véletlenszerű események. Ma ez egy teljes tudomány, amely nagy gyakorlati jelentősége van.
A történelem valószínűségszámítás nyúlik vissza, a XVII században, amikor az első kísérlet szisztematikus kutatási feladatokat végeztünk kapcsolatos tömeges véletlenszerű jelenségek és a megfelelő matematikai apparátus. Azóta sok alapítvány fejlesztettek ki és mélyült a jelenlegi elképzelések más fontos törvények és törvényszerűségek nyíltak. Sok tudós dolgozott és dolgozik a problémák az elmélet a valószínűség.
Közülük lehetetlen nem kell figyelni, hogy a munkálatok a Simeon Poisson Denis ((1781-1840) - francia matematikus) bizonyult általánosabb, mint a Yakova Bernulli, a forma, a nagy számok törvénye, és az első, hogy alkalmazza az elmélet a valószínűség, hogy a problémákat a tűz. Poisson neve kapcsolódik az egyik az elosztó törvényeket, amely fontos szerepet játszik a valószínűségszámítás és alkalmazásai.
Ez a törvény úgy is leírható, mint korlátozó esetében binomiális eloszlás, ha a valószínűsége p esemény mi érdekli egyetlen kísérlet nagyon kicsi, de a kísérletek számát m előállított egységnyi idő alatt elég nagy, és ez az, hogy a folyamat p
Op munka hajlamos pozitív konstans értéket
).
Ezért a Poisson jog gyakran nevezik a törvény ritka események.
Raspredelenie Puassona a valószínűségszámítás
Funkció és számos elosztási
Raspredelenie Puassona - egy speciális esete a binomiális eloszlás (n >> 0 és p -> 0 (ritka esemény)).
Matematika ismert formula becsült értékének kiszámításához bármely tagja a binomiális eloszlás:
ahol a = n · p - Poisson paraméter (elvárás), és a diszperziót egyenlő a várakozást. A matematikai számítások átmenetet magyarázó. binomiális eloszlás
írhatók, ha meghatározott p = a / n. formájában
Mivel p nagyon kicsi, meg kell, hogy vegye figyelembe a számot csak a m. összehasonlítva kicsi n. termék
igen közel van egyhez. Ugyanez vonatkozik az értéke
nagyon közel az e -a. Ennélfogva, megkapjuk a képlet:
Euler-féle szám (2,71 ...).
,
generáló függvény
A kumulatív valószínűség-eloszlás
Számos eloszlása az X valószínűségi változó szerint vannak elosztva a Poisson jog, az alábbiak szerint:
,
.
Példa feltételek, amelyek mellett nincs Raspredelenie Puassona
Mint már említettük, sok gyakorlati probléma vezet Poisson-eloszlású. Vegyük az egyik ilyen tipikus feladatokat.
Legyen az x tengely Ox véletlenszerűen elosztott pontot (3.). Tegyük fel, hogy egy véletlenszerű eloszlását pontok megfelelnek az alábbi feltételeknek:
1) a valószínűsége, hogy egy adott számú pontot az intervallum l függ csak a hossza ebben a szegmensben, de nem függ pozícióját az abszcisszán. Más szóval, a pontok vannak elosztva az abszcissza az azonos átlagos sűrűsége. Jelöljük ezt a sűrűséget, azaz a elvárás a pontok száma egységnyi hosszán keresztül # 955; .
2) pont elosztva a vízszintes tengelyen egymástól függetlenül, azaz a valószínűsége ütő egy bizonyos számú pontot egy adott időszakban nem függ, hányan kapott bármely más szegmense átfedés nélkül velük.
3) a valószínűsége, hogy egy kis részét # 916, a két vagy több pont elhanyagolhatóan kicsi a valószínűsége, hogy egy ponton (ez az állapot gyakorlatilag lehetetlen egybeesés két vagy több pont).
Isolate az abszcissza bizonyos szegmens hossza l, és megvizsgálja a diszkrét véletlen X változó - a pontok száma eső ez a darab. A lehetséges értékek az értékek 0,1,2, ..., m, ... Mivel a pontok esnie egy szegmens függetlenül, akkor elméletileg lehetséges, hogy lesznek-e olyan szám, azaz A sorozat folytatódik a végtelenségig.
Azt bizonyítja, hogy az X valószínűségi változó Poisson eloszlás. Erre a célra kell számítani a valószínűsége, hogy a Pm szegmens esik pontosan m pont.
Először oldjuk meg a problémát egyszerűbb. Tekintsük az Ox kis részét # 916; s, és kiszámítja a valószínűsége, hogy ez a hely, hogy legalább egy pontot. Mi a következőképpen kell eljárni. A várható pontok száma eső oldalon nyilvánvalóan még mindig # 955, # 903, # 916; .. X (t egységnyi hosszúságú, hogy átlagosan ítélik # 955; pontok). Szerint a 3. feltétel egy kis szegmens # 916; x lehet hanyagolni a lehetőséget eső rajta két vagy több pont. Ezért az elvárás # 955, # 903, # 916; x pontok száma eső rész # 916; s. megközelítőleg egyenlő a valószínűsége, hogy egy pontot rajta (vagy ezzel ekvivalens, legalább egy az adott körülmények között).
Így akár végtelen kis magasabb rendű, az # 916; x → 0, akkor feltételezhetjük valószínűsége, hogy a webhely # 916; s kap egy (legalább egy) pont megegyezik az # 955; # 903; # 916; s. és annak a valószínűsége, hogy az egyik nem fog semmilyen 1-c # 903; # 916; s.
Mi ezt kiszámítani a valószínűsége, ütő az intervallum Pm l pontosan m pont. Osszuk a szegmens L egy n hosszúságú egyenlő részekre
Nézzük megállapodnak, hogy hívja az elemi szegmens # 916; s „üres”, ha nem kap pontot, és a „foglalt”, ha legalább egy találatot benne. Szerint a fent bizonyítottak a valószínűségét, hogy a szegmens # 916; s lesz „foglalt” megközelítőleg egyenlő # 955; # 903; # 916; X =
; a valószínűsége, hogy ő lesz az „üres”, értéke 1
. Mivel, feltétel szerint 2, pont tartozó, nem-átfedő szegmenst függetlenek, akkor a mi n szegmensek lehet tekinteni, mint a független n „kísérletek”, amelyek mindegyikében a szegmens lehet „foglalt” p valószínűséggel =
. Nézzük mi annak a valószínűsége, hogy többek között n szegmensek lesz pontosan m «elfoglalt». Az ismételt vizsgálatok független tétel, ez a valószínűség
,
.
Elég nagy n, ez a valószínűség kb egyenlő a valószínűsége, hogy a szegmens pontosan l m pixel, m. K. Első két vagy több pontján egy szegmens # 916; s egy elhanyagolható. Ahhoz, hogy megtalálja a pontos értékét Pm. el kell menni a határ n → ∞ esetén:
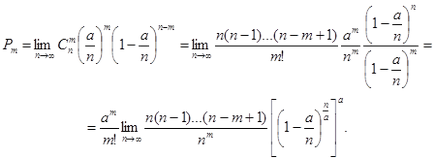
,
azt találjuk, hogy a megkívánt valószínűséggel adják
ahol a = # 955; l. azaz X változó megfelelően oszlanak Poisson eloszlást a = # 955; l.
Meg kell jegyezni, hogy a nagysága és az értelemben jelenti az átlagos száma kapcsolódó pontok az intervallum l.
Az érték R1 (a valószínűsége, hogy a X változó vesz pozitív érték) ebben az esetben kifejezi a valószínűsége, hogy az intervallum l eléri legalább egy ponton: R1 = 1-e-a.
Így azt találtuk, hogy a Raspredelenie Puassona merül fel, ha egy bizonyos ponton (vagy más alkatrész) foglalnak egy tetszőleges helyen egymástól függetlenül, és számolja a pontokat, hogy ebbe néhány régióban. A mi esetünkben, ezen a területen volt egy szegmens L az x-tengelyen. Ez a következtetés azonban könnyen kiterjeszthető a forgalmazás esetében pont a síkon (lapos mez® pont) és térben (térbeli pont véletlen mező). Könnyen bizonyítani, hogy ha a feltételek:
1) pont oszlanak statisztikailag egységes mező átlagos sűrűsége # 955; ;
2) pontok tartoznak a nem-átfedő régió egymástól függetlenül;
3) pont jelenik meg külön és nem párban, háromágyas, stb
A pontok száma X. bármekkora régió D (síkbeli vagy térbeli) szerint vannak elosztva a Poisson törvény:
,
és ahol - az átlagos pontok száma eső régióban D.
A Poisson eloszlás a pontok száma alá egy szakasz vagy szegmens, a feltétel az állandó sűrűségű (# 955; = const) nem lényeges. Ha két eltérő körülmények között a Poisson jog egyébként csak akkor következik be, és lehetőséget válik egy másik kifejezéssel: ez nem olyan egyszerű, sűrűség szorzás # 955; A hossz, terület vagy térfogat, és az integrációs változó sűrűségű mentén szegmens, területet vagy térfogatot.
Esettanulmányok
1. A berendezés áll 1000 elemek felhasználásával egymástól függetlenül. A meghibásodási valószínűség bármely elemének időn belül T egyenlő 0,002. Annak a valószínűsége, hogy az idő nem volt hajlandó T pontosan három eleme van.
Határozat. mert azzal a feltétellel, n = 1000 elég nagy, és m = 0,002 kicsi, tudjuk használni a Poisson eloszlás:
Határozat. Események „ez a hatás volt megfigyelhető legalább egyszer” (jelöljük P), és az »ez a hatás nem volt megfigyelhető, még egyszer« (jelöljük Q), nyilván vannak ellentétes. Ezért a P + Q = 1. ahonnan
Azzal a feltétellel, P = 0,95. ezért
Így a kívánt átlagos száma vizsgálandó minták, - 300 db.
3.Veroyatnost egy nyertes lottószelvény p = 0,01. Hogyan jegyet nyer legalább egyikük valószínűséggel P nem kevesebb, mint 0,98?
Határozat. Annak a valószínűsége, győztes alacsony, és a jegyek számát a megvásárolni kívánt nyilvánvalóan nagy, így egy véletlen számot nyerő jegyek mintegy Raspredelenie Puassona.
Események „sem a megvásárolt jegy nem a győztes” és a „legalább egy jegy - nyertes” - az ellenkezője. Ezért az összeget a valószínűsége ezek az események egyenlő egy:
Ezzel a feltételezés, R≥0,98. vagy 1-e -s ≥0,98. Ahol f s ≤0,02.
A táblázatból azt látjuk, e -3.9 = 0,02. mert függvény e -x - csökken, az előző egyenlőtlenség igaz a≥3,9. vagy np≥3,9. Ezért n≥3,9 / 0,01 = 390.
Így meg kell vásárolni legalább 390 jegyet nyer legalább az egyiket.
4. Másodlagos hívások számát, hogy az alközpont egy perc alatt egyenlő 120. annak a valószínűsége, hogy két másodperc alatt az alközpont nem volt hívás; két másodpercig a csere megy legalább két hívást.
Határozat. két másodpercig hívások átlagos száma a következő:
Annak a valószínűsége, hogy az állomás 2-másodpercig nem volt hívás:
Esemény álló részesülő legalább két hívás azt jelenti, hogy az állomás nem kaptak egyetlen hívást vagy a bevitt egyetlen. Tehát annak a valószínűsége egy kevesebb, mint 2-hívások ugyanakkor egyenlő:
5.Sluchaynaya X változó - az elektronok száma kibocsátott egy fűtött katód egy elektroncső t idő, # 955; - az átlagos száma emittált elektronok időegységenként. Határozza meg a valószínűsége, hogy a t időpontban a száma kibocsátott elektronok kisebb, mint m (mÎN).
Határozat. # 955; - az átlagos elektronok száma, t - az emissziós időtartam tehát a = # 955; t.
6. fűtött katód kibocsátott egységnyi idő átlagosan q (t) az elektronok ahol t - idő eltelt, a kísérlet kezdetén. Annak a valószínűsége, hogy az időintervallum időtartamára # 964;, kezdve a T0 időpontban, a katód elektronok repülnek pontosan m.
Határozat. Találunk az átlagos elektronok száma is. eltérnénk a katód ebben az időszakban az idő:
A számítások szerint, és meghatározza szükséges valószínűsége:
Összefoglalva, azt látjuk, hogy Raspredelenie Puassona gyakori és fontos értékesítési rendelkező alkalmazások az elmélet a valószínűség és alkalmazásai, valamint a matematikai statisztika.
Sok gyakorlati problémák csökkennek, végül a Poisson eloszlás. Különlegessége, ami abból áll, hogy az egyenlőség, a várható értéke és szórása, gyakran használják a gyakorlatban, hogy megoldja a problémát, egy valószínűségi változó által forgalmazott Poisson törvény, vagy sem.
Szintén fontos az a tény, hogy a Poisson törvény lehetővé teszi a valószínűsége események ismételt független vizsgálatok nagyszámú ismétlések tapasztalat és egy kis egység a valószínűség.
Irodalom