A görbületi és a görbületi sugár

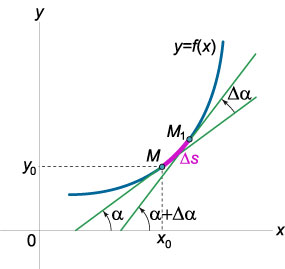
Tekintsünk egy sík által meghatározott görbe a következő egyenlettel \ (y = f \ left (x \ jobbra). \) Tegyük fel, hogy a ponton \ (M \ left (\ right) \) tartott érintőleges ez a görbe, amely szöget \ (\ alpha \) és a vízszintes tengely (ábra \ (1 \)). At elmozdulás \ (\ Delta s \) körív mentén egy görbe pont \ (M \) pontba mozgat \ (\). A helyzet az érintő is változik: a dőlésszög az érintő a tengely \ (Ox \) pontnál \ (\) lesz legyen \ (\ alpha + \ Delta \ alpha. \) Ezért, ha (\ Delta s \) elmozdulása a pont a görbe távolságban \ érintőleges forog \ (\ Delta \ alpha. \) (Tegyük fel, hogy a szög \ ( \ alpha \) növekszik az óramutató járásával ellentétes forgás.)

Az abszolút értéke az arány \ (\ nagy \ frac >> \ normalsize \) az úgynevezett átlagos görbülete az ív \ (M. \) A határértéket, a \ (\ Delta s \ 0 \), megkapjuk a görbület a görbe azon a ponton, \ (M: \) \ [K = \ lim \ limits_ \ left | >>> \ right |. \] Ebből a meghatározásból az következik, hogy a görbület bármely pontján a görbe jellemzi a forgási sebessége az érintő ezen a ponton.

Egy síkgörbe \ (y = f \ left (x \ right) \) görbületi ponton \ (M \ left (\ right) \) fejeződik ki az első és a második deriváltak függvény \ (f \ left (x \ right) \) a képlet \ [K = \ frac \ right | >> \ right)> ^ 2 >> \ right]> ^ \ normalsize >>>> \] Ha a görbe adott paraméteres egyenletek formájában \ (x = x \ left (. t \ jobbra), \) \ (y = y \ bal (t \ jobbra), \) a görbületi bármely ponton \ (M \ left (\ right) \) egyenlő \ [K = \ frac \ right |> > \ right)> ^ 2> + \ right)> ^ 2 >> \ right]> ^ \ normalsize >>>>. \] ha a görbe adott egyenlete polárkoordináták \ (r = r \ left (\ theta \ jobbra), \) a görbület által adott \ [K = \ frac + 2 \ right)> ^ 2> - rr ''> \ right | >> + \ right)> ^ 2 >> \ right]> ^ \ normalsize >>>>. \] a görbületi sugár a ponton kapott görbét \ (M \ left (\ right) \) az úgynevezett inverz görbületi \ (K \) adott görbe az adott ponton: \ [. R = \ frac \] Következésképpen, síkbeli görbék adott explicit egyenlet \ (y = f \ left (x \ right), \) sugara görbületi ponton \ (M \ left (\ right) \) kell adni a kifejezést \ [R = \ frac \ right)> ^ 2 >> \ right]> ^ \ normalsize >>>> \ right | >> \].

Számítsuk ki a görbület a ellipszis \ [\ frac >>>> + \ frac >>>> = 1 \] annak csúcsait.

Nyilvánvaló, elegendő megállapítani, hogy az ellipszis görbület pontokon \ (A \ left (\ right) \) és \ (B \ left (\ right) \) (ábra \ (2 \)), hiszen a szimmetria a görbe görbület két szemközti csúcsa ellipszis ugyanaz lesz.

Kiszámításához a görbület kényelmes elmozdulni az ellipszis kanonikus egyenlet a következő egyenlet paraméteres formában. \ [X = a \ cos t, \; \; \; y = b \ sin t \.] Amennyiben \ (t \) - egy paramétert. Pontban \ (A \ bal (\ right) \) paraméter beállítása \ (t = 0, \), és azon a ponton, \ (B \ bal (\ right) \) annak értéke \ (t = \ nagy \ frac \ normalsize. \)

Megtalálni a görbülete és görbületi sugara a parabola \ (y = \) a származási.

Find a görbülete és a görbületi sugara a görbe \ (y = \ cos mx \) a maximum pont.

Ez a funkció érik el maximális pontok \ (x = \ nagy \ frac> \ normalsize, \; n \ Z. \) periodicitása görbületi minden pontban azonos maximális, így elegendő figyelembe venni egyetlen pont \ (x = 0 \).