Grafikonok, példák és gyakorlatok

Grafikonok származott a tizennyolcadik században, amikor a híres társ-Matic, Leonhard Euler, próbálta megoldani a problémát ma már klasszikus Kőnigsbergi hidak. Abban az időben volt két ostrova kapcsolódik hét hidat Pregol bankok a folyó és egymással Kenigsber-n ábrán látható. 7.1. 3adacha with-a következő: végezzen egy sétát a városban, így elhagyása után pontosan egyszer minden hidat, hogy visszatérjen az ugyanazon a helyen, ahol a séta kezdődött. E probléma megoldása, Euler Königsberg ábrázolt, mint egy grafikon, azonosítja azt a felső részét a város, és az élek - a hidak, amelyek ezekhez a részek. Ahogy azt mutatják §-ban 7,1, Euler sikerült igazolni, hogy a kívánt útvonal elkerüli a város nem létezik.

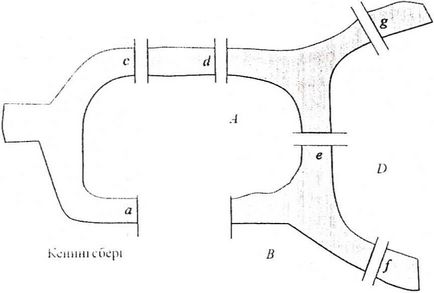
Ábra 7.1. Scheme régi Königsberg

Ebben a fejezetben bemutatjuk a terminológia használatos gráfelmélet, és megérteni néhány konkrét feladatokat megoldani segítségével grafikonokat. Különösen megnézzük az osztály grafikonok nevezett fák. Fák - természetes modellt képviselő az adatok szervezett hierarchikus rendszerben. Keresés a fa elkülönítésére egyes objektumok és válogatás adatok egy fa az egyik fő fókuszpont a számítástechnikában. A Függelék a fejezetben fogunk foglalkozni válogatás és adatok lekérdezéséhez, rendezett fák.

Ábra. 7.1 ábra a hét Konigsberg hidak úgy. volt található a XVIII. A probléma, amelyre obpa-tilsya Euler, az a kérdés: Találhatunk egy útvonalon gyalogos, társ-tory fut pontosan egyszer minden a hidak és kezdődik és végződik, ugyanazon a helyen a városban?

feladat modell - egy grafikon, amely egy több csúcsok és több összekötő élek a csúcsok. A csúcsokat A, B, C és D szimbolizálja a folyóparton és a szigetek, és a széleket egy, a. c, d, f és g jelöli a hét hidat (lásd. ábra. 7.2). Keresek az útvonalat (ha létezik) felel meg áramköri szélei gráf úgy, hogy mindegyikük vezetünk csak egyszer. Bordákkal nyilvánvalóan megfelel a kereszteződésekben a folyami híd.

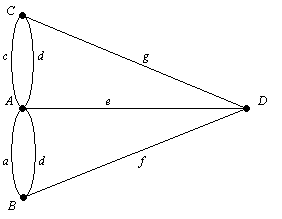
7.2 ábra. modellje a probléma a hidak Königsberg

Grafikont, amelyben van egy ösvény, van egy út a rank-és ér véget a két csúcsot, és kiterjed minden éle a gráf pontosan egyszer hívjuk zylerovym grafikonon. Sequence-ver gumiabroncs (esetleg ismétlések), amelyen keresztül halad ISCO-én az útvonalon, mint az útvonal maga hívják eylerovymtsiklom. Euler megjegyezte, hogy ha a gráf egy Euler ciklus, akkor minden él, ami néhány vertex kell találni minden éllel a vertex 1 és nyert az egyszerű nablyudsniya ezt a következtetést: ha ez az oszlop létezik Euler ciklus ezután minden egyes vertex alkalmasnak kell lennie páros számú élek.

Ezen túlmenően, Euler volt képes bizonyítani az ellenkezőjét állítást, ábrázolás, így a grafikon, amelyben minden pontpár van kötve nem-sorozata élek Euler akkor és csak akkor, ha minden csúcsának még fokozatot. A mértéke a v csúcs az a szám, δ (v) a bordák, ez intsidentnyh2.

Most már egyértelmű, hogy a gráf modellezése a problémát a hidak Königsberg, Euler ciklus nem található. Valóban, de a mértéke a csúcsok páratlan: δ (B) = δ (C) = δ (D) = 3, és a δ (A) = 5. A könnyen grafikonok Euler kézzel, hasonló ahhoz, amely megvizsgáltuk, hogy megoldja a problémát a hidak, acél használat- megoldásában számos gyakorlati problémák és a tanulási nőtt jelentős terület a matematika.

Egyszerű gráf úgy definiáljuk, mint egy pár G = (V, E), ahol V - egy véges csúcsok halmaza és E - véges halmaza bordák, mint lehet-tartalmaznak hurkok (élek, hogy kezdődik és Zakan-kü- egyik csúcsa) és a többszörös bordák (úgynevezett többszörös vayutsya több összekötő élek ugyanazt a pár csúcsok). A grafikon ábrán látható. 7.2. Ez nem egyszerű, mivel például, csúcsok az A és B csatlakozik két borda (csak ezek a szélek nevezik multiplex).

Két csúcs u és v egy egyszerű gráf nevezzük szomszédos. ha csatlakoztatva néhány e élét. amiről azt mondják, hogy az eset, hogy az u csúcs (v). Így tudjuk representat-vlyat jelenleg beállított E élek, mint egy sor pár szomszédos csúcsok, ezáltal definiálva nem reflexív, szimmetrikus reláció V. A hiánya visszaható annak a ténynek köszönhető, hogy egy egyszerű gráf nincs hurkok, T. E. Reber, mindkét végén amelyek ugyanabban a tetején. A szimmetria a kapcsolat abból a tényből fakad, hogy az e élen. Csatlakozó felső és v, v, és kapcsolódik a és (más szóval, a bordák nem orientált, ez van. E. Ne irányban). Az egyetlen él olyan egyszerű gráf, amely összeköti a pontpár u és v, jelöljük hogyan és v (vagy vulgaris).

Logic mátrix kapcsolatot a csúcsok halmaza, meghatározott kotopoe széle, úgynevezett szomszédsági mátrix. A szimmetria kapcsolatok szempontjából a szomszédsági mátrix M ÓZNA-chaet hogy M szimmetrikus az fő átlós. És mivel a nem-reflexivitás e kapcsolat a fő diagonális mátrix M jelentése szimbólum „L”.

Példa 7.1. Rajzoljunk egy gráf G (V, E) a csúcsok halmaza V = és élhalmazok E =. Írja le a szomszédsági mátrix.

Határozat. Egy gráf ábrán látható. 7.3.

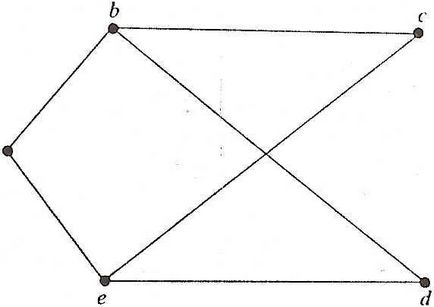
A szomszédsági mátrix a következő formában:

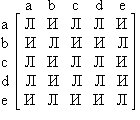
Helyreállítani a grafikon már csak az elemek a szomszédsági mátrix, amely felett állnak a fő átló.

Részgráfja G = (V, E) a G gráf '= (V', E '), ahol E' C E és V „C V.

7.2 példa: A diagramok között H, K és L, ábrán látható. 7.4 részgráfok G.

Határozat. Jelöljük a csúcsai gráf G, H és K ábrán látható. 7.5. Grafikonok a H és K - részgráfok G, amint a mi jelöléssel. Earl L nem egy részgráfját G, mert a csúcsra az index 4, és a G gráf nincs ilyen.

Ábra 7.9. Egy példa a Hamilton-gráf

Határozat. Tegyük fel, hogy egy gráf talál Hamilton kör. Minden csúcs v benne van a Hamilton-kör a választás a két él esemény rá, és ezért azt a mértéket minden csúcsa a Hamilton kör (eltávolítása után a felesleges élek) egyenlő 2. A mértéke a gráf - 2 vagy 3. A csúcsok mértéke 2 tartalmaz egy gyűrű együtt mindkét eset velük bordákkal. Következésképpen, az élek ab, ae, CD, CB, hi, hg ij és egy adott sorrendben tartalmaz egy Hamilton kör C (lásd. Ábra. 7.10.).

Bf borda nem lehet része a ciklus S. mivel minden csúcsa a ciklus kell egy bizonyos fokú 2. Tehát a bordák és a fi fg szükséges, hogy kössön hurkot C. hogy tartalmazza a vertex f. De aztán a bordák és a je gd semmiképpen nem tartoznak a S. ciklus, mert különben ez lesz a csúcsok foka három. Ez arra kényszerít bennünket, hogy tartalmazza a ciklusban borda ed. ami ellentmondás: a bordák, kénytelenek voltunk választani formában két leválasztott ciklus helyett, amelynek létezését vártuk. Következtetés: A grafikon ábrán látható 7,10, nem Hamilton.

Hamilton grafikonok modellezéséhez használt számos gyakorlati problémát. Az alapja az összes ezeket a problémákat egy klasszikus utazó ügynök probléma.

Eladó kell bejárjuk a várost, és vissza, miután tartózkodott minden városban pontosan egyszer, ugyanakkor a költségek csökkentése az utazás a lehető legkisebb.

Ábra 7.10. A bordák szerepel a Hamilton kör C

Grafikus modellje az utazó ügynök probléma Hamilton gráf, amelynek csúcsai képviseli a várost, és a széleit összekötő út számukra. Ezen kívül minden éle van szerelve egy súlyt jelzi a szállítási költségeket kell utazni a megfelelő módon, így például a távolságot a városok vagy vezetés közben az úton 2. A probléma megoldása érdekében meg kell találnunk egy Hamilton-kör minimális összsúlyú.

legközelebbi szomszéd algoritmus.

Ez az algoritmus termel szuboptimális megoldást TSP generáló Hamilton ciklusokat a betöltött oszlopot több csúcsú V. A ciklus műveletben kapott az algoritmus, egybeesik a végső érték a változó útvonal, és annak teljes hossza - végleges értéke változó w.

whileostayutsya jelöletlen vershinydo

Válassza jelöletlen vershinuu,

Ennek eredményeként, az algoritmus találtak Hamilton DCABD teljes tömege a ciklus 24. készítése kimerítő keresés Az összes ciklus ebben a kis dobozban megtalálható két másik Hamilton kör: ABCDA teljes tömege 23 és a teljes tömege ACBDA 31. A teljes gráf húsz csúcs létezik körülbelül 6 1 10 16 Hamilton ciklus, átadása, amely előírja, nagyon sok időt és számítógép memóriájában.

Mint már említettük, van egy osztály a grafikonok nevezett fák, amelyeket különösen széles körben használják a számítógépes alkalmazások. Egy gráf G = (V, E) az úgynevezett egy fa. ha csatlakoztatva van, és gyűrűs (azaz. nem tartalmaz ciklus).

Legyen G = (V, E) - Count cn csúcsok és m élek. Lehetőség van megfogalmazni számos szükséges és elégséges feltételeket kotoryhGyavlyaetsya fa:

Bármilyen pár csúcsok Gsoedinena egyetlen út.

Gsvyazen, és eltávolítjuk legalább egy bordája sérti a összekapcsolódás a grafikonon.

Gatsiklichen, de ha hozzá legalább egy éle, akkor vGpoyavitsya ciklust.

Az egyenértékűség többségének ezek a feltételek könnyen beállítható. A legnehezebb, hogy foglalkozik a második közülük. A következő példában, azt mutatják, hogy egy fa n csúcsú pontosan n- 1 élek.

Példa 7.7. Igazoljuk indukcióval a csúcsok száma, hogy derevaT csúcsok és m cn bordák kielégítése a összefüggést: m = n-1.

Határozat. Mivel a fa egyetlen csúcs nem tartalmaz élek, akkor az az állítás igaz n = 1.

Tekintsünk egy T fa cn csúcsok (élek és m), ahol n> 1, és feltételezik, hogy minden fa, k

Távolítsuk el a szélén T. A harmadik tulajdonság derevoT után ez az eljárás válik egy szétkapcsolt grafikon. Kap pontosan két csatlakoztatott készülékek, amelyek közül egyik sem nincs ciklus (különben az eredeti graft tartalmazna túl ciklust, és nem lehetett egy fa). Így a csatlakoztatott komponensek - azonos fák.

Az indukciós feltevés fa T1 imeetn1 - 1 borda AT2-N2 - 1. Következésképpen, a kiindulási derevoT alkalmaz (tekintve egy távoli)

Ez könnyű bizonyítani, hogy minden gráf van egy részgráf, amely egy fa. Részgráfjában Ez egy fa, és tartalmazza az összes vershinyG. nazyvaetsyaostovnym fa. Feszítőfának a grafeGstroitsya egyszerű: válasszon egy tetszőleges él, és azt következetesen hozzá a többi élek kialakítása nélkül ciklust, amíg nem lesz hozzá az éleket, anélkül, hogy ebben a ciklusban. Hála a 7.7 példa, tudjuk, hogy építeni egy feszítőfának a grafikonon csúcsok IZN kell választania rovnon - 1 él.

Példa 7.8. Keresse meg a két különböző feszítőfa a kavicságyba, ábrán látható. 7.12.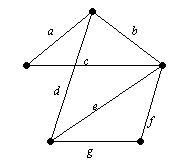

Ábra 7.12. Connected G gráf

Határozat. A grafikonon, több feszítőfa. Egyikük úgy kapjuk egymást követő szelekciós élek: a, b, d, mint f. Egyéb - b, c, e és g. Úgynevezett fák ábrán mutatjuk be 7,13.

A példában leírt eljárással 7,8 lehet igazítani a legrövidebb megoldások vegyületek feladatok:

Ki kell építeni a vasúti összekötő hálózat több városban. Ismert építési költségének a szegmens utak mindegyike között városokban. Szükséges, hogy megtalálják a legkisebb költséggel hálózat.

A nyelv a gráfelmélet, meg kell találnunk a betöltött grafikon feszítőfát legkisebb összsúly. Egy ilyen fa az úgynevezett minimális feszítőfa, röviden MOD. Ezzel szemben az utazó ügynök probléma, van egy hatékony algoritmust, amely megkeresi valóban a minimális feszítőfa. Ez hasonló az algoritmus Prima.

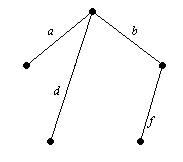
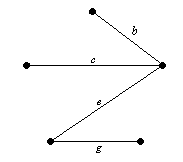
Ábra 7.13. Feszít®fája G

A keresési algoritmus minimális feszítőfa. Legyen G = (V, E) - csatlakoztatott súlyozott gráf. MOD algoritmus létrehoz egy G gráf választotta a lehető legkisebb súly éleket egy feszítőfa. MOD a számítógép memóriájában tárolt, mint egy több T élek.

e: = borda grafaGs legkisebb súlyú;

Határozat. A bordák vannak kiválasztva a következők: Először - 1 DE 2 tömeg; második - AC súlya 3; a harmadik - a CE 7. súlya ebben a szakaszban építés alatt fa úgy néz ki, mint az ábrán. 7.14

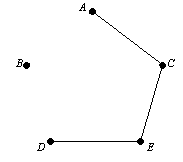
Ábra 7.14. Fa nézet után három lépésben

Kell hung borda - AD, AE és CD, amelyek mindegyike súlya 9. Azonban bármelyik közülük már nem adunk, viszont a ciklus. Ezért jegyzett bordák ki kell zárni a rendelkezésre áll. Ezután jönnek a nap bordák és súlya BD 11. Akkor csatolja ezek közül bármelyik, míg a fogadó két különböző MOD: súly vagy 23 minden.

Gyakran előfordul, hogy szeretnénk, hogy a fák, amelyek alapján a természetes kialakulását hierarchikus struktúrák, mint például a, például, családfa (ris.7.15). Ez azt mutatja, néhány tagja a Bernoulli család, akik mindegyike egy híres svájci matematikus.

A családfát is képviselteti tömörebben. A rendszer ábrán 7,16 példája az úgynevezett fa gyökere. Fa gyökér egy fa egy speciális csúcsuk. Ez az elkötelezett vertex és a gyökér a fa. A fa tetején, amely közvetlenül a gyökér, az úgynevezett fia. Másrészt, top, állva közvetlenül előtte fia hívott apja.